A Level Maths: Solving complex quadratic equations
18 February 2021
Hints and tips - 10 minute read
 Steven Walker, OCR Maths Subject Advisor
Steven Walker, OCR Maths Subject Advisor
In my previous blog I looked at using graphs to investigate quadratic functions. I’m now going to look at some of the issues seen by examiners as the complexity of the quadratic increases.
Using the same set of techniques developed for quadratic equations we can solve a range of equations, such as polynomial, exponential and trigonometric equations.
In A Level Maths there is an emphasis on mathematical reasoning; how the answer is obtained is just as important as the answer itself.
Use of calculators
Many of the calculators allowed for maths exams include a function to solve quadratics. There is no restriction in using this function, although students may sometimes be able to solve standard quadratic equations by inspection just as quickly.
The standard three term quadratic
Students will be familiar from GCSE (9-1) Maths with equations such as 2x2 + 5x – 7 = 0, a standard three term quadratic that could be solved by:
- factorising (x – 1) (2x + 7) = 0,
- completing the square 2 (x + 1.25)2 – 10.125 = 0, or
- the quadratic formula
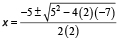
Over the years, examiners have reported students making more errors when attempting to substitute values into the quadratic formula than with the other two methods.
Some candidates appear to ‘reverse engineer’ their factorisation from the calculator. Here, misconceptions about the link between factors and roots are often seen, such as either the incomplete (x – 1) (x + 3.5) = 0 or incorrect signs (x + 1) (2x – 7) = 0.
Similarly, attempts to ‘reverse engineer’ the completed square format from the calculator often result in sign errors with the term either inside or outside the bracketed term, or missing the leading multiplying factor.
Examiners will check the working that is presented alongside a final answer. In mark schemes, ‘www’ (‘without wrong working’) means that subsequent accuracy marks cannot be awarded when the method is incorrect, resulting in M0A0.
More complex polynomials
The equation 2y + 5√y – 7 = 0 can be reduced to the standard quadratic by using the substitution ‘Let x = √y’.
Candidates need to be aware that explicitly stating the substitution or the justification for rejecting roots are part of a clear mathematical argument. In this case the solution would need to include the statement ‘x ≠ -3.5 since √y ≥ 0’.
Examiners have noted that students make fewer arithmetic errors when using the clear substitution method rather than trying to find the factorised form, i.e. (2√y + 7) (√y – 1) = 0.
A similar approach can be taken for the equation 2x4 + 5x2 – 7 = 0, using a substitution such as ‘Let X = x2’. Here it is important to not only state ‘X ≠ -3.5 since x2 ≥ 0’, but also to remember to finish the solution with ‘x2 = 1, so x = ± 1’.
Graphing can help demonstrate when roots may need to be rejected (see disguised quadratic on Desmos).
Note that it is good practice to make a clear distinction between the initial equation variable and the variable used in the substitution version.
Exponential equations
Students should be able to recognise the standard three term quadratic format when the equation has the unknown as the exponent.
While factorising 3e2x + 14ex – 5 = 0 to (3ex – 1) (ex + 5) is a valid method, examiners report that a substitution such as X = ex often yields fewer mistakes.
Equations such as 32x – 3x – 2 = 0 can be solved by different routes, but again success is seen more often when using a substitution such as X = 3x.
These questions will often explicitly ask for the solution to be given as an exact value in a specific form such as ‘giving your answer in the form x = a logb c, where c > 1’, with the final accuracy mark awarded for manipulating into this required form.
Trigonometrical equations
The third type of disguised quadratic equation is found in trigonometric equations, such as 5 cos 2θ cosec θ = 2. The first step is often changing the trigonometric functions into a single form using standard Pythagorean identities to give, for example, 10sin2 θ + 2sin θ – 5 = 0.
Examiners note that mistakes often occur when students attempt too many steps at once. Here, a sensible set of steps might use cosec θ = (sin θ)-1 on one line, the identity cos 2θ = cos2 θ – sin2 θ on a separate line and the identity cos2 θ = 1 – sin2 θ on another line of working.
After manipulating the trigonometry, the next steps could be using a substitution to state ‘Let X = sin θ’, solving the resulting quadratic and finally substituting back to find θ.
An important point to remember when solving trigonometrical equations is any defined domain restrictions, such as – π < θ < π, 0 ≤ θ < 2π, or perhaps 0 ≤ θ < π in radians or the equivalents in degrees.
Full marks may not be awarded if an answer includes additional responses outside of the restrictions defined in the question. A sketch is a useful aid to avoid dropping these accuracy marks at the end (see this trig equations demonstration on Desmos).
More support
Our ‘bridging the gap’ guide includes suggestions for work that can be done early in year 12 to recap algebra covered at GCSE.
For a range of exam questions, see the practice and past papers on Interchange and our webpages for Mathematics A H230/H240 and Mathematics B (MEI) H630/H640. Also available from these pages are our examiners’ reports, which include notes on common mistakes and misconceptions.
ExamBuilder is a useful tool for quickly sourcing questions on specific topics. You can use its filters to find appropriate questions, along with their mark scheme and examiner report comments. See our ExamBuilder guide for support in adapting legacy questions for current students. You may also enjoy our Friday Maths puzzles posts on @OCR_Maths using #OCRmathsPuzzle. Here’s a recent example investigating an equation with the unknown as the exponential:
Find a value of x to solve the following equation:
83x+2 - 83x = 1008
Stay connected
There are so many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
If you have any questions, email us at maths@ocr.org.uk, call us on 01223 553998 or Tweet us @OCR_Maths. You can also sign up for email updates to receive information about resources and support.
About the author
Steven joined OCR in 2014 during the major qualification reform period and now primarily focuses on supporting the Level 3 maths qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas. He is currently balancing his ‘work from home’ commitments with supporting his daughter with her year one lessons.
By the same author