A Level Maths: what do we mean by “Show that” questions?
02 December 2024
Steven Walker, Maths Subject Advisor

Both of our A Level Maths suites make use of a defined list of question commands to provide exam room guidance to the level of written response needed to answer each question. Full details can be found in the specifications, with additional guidance in our “Exploring the Question Paper” (Spec A and Spec B) documents and also summarised in our command word poster.
“Show that”
The specification defines the question command prompt “show that” as:
“Learners are given a result and have to show that it is true. Because they are given the result, the explanation has to be sufficiently detailed to cover every step of their working”.
To assess mathematical reasoning
The assessment objective AO2 includes the requirement to set questions that allow candidates to demonstrate the ability to “construct rigorous mathematical arguments”, “explain their reasoning” and also demonstrate they can “use mathematical language and notation correctly”.
In these questions it is important for students to not only show the maths, but also to justify how their maths has actually shown that the statement is true.
Question 9 H640/01 2023

All three parts of this question have a significant focus on mathematical language and notation of gradient functions. By giving the answer in parts (a) and (b) students that struggled with either part can still progress to the final part.
Q9 H640/01 2023 Mark scheme
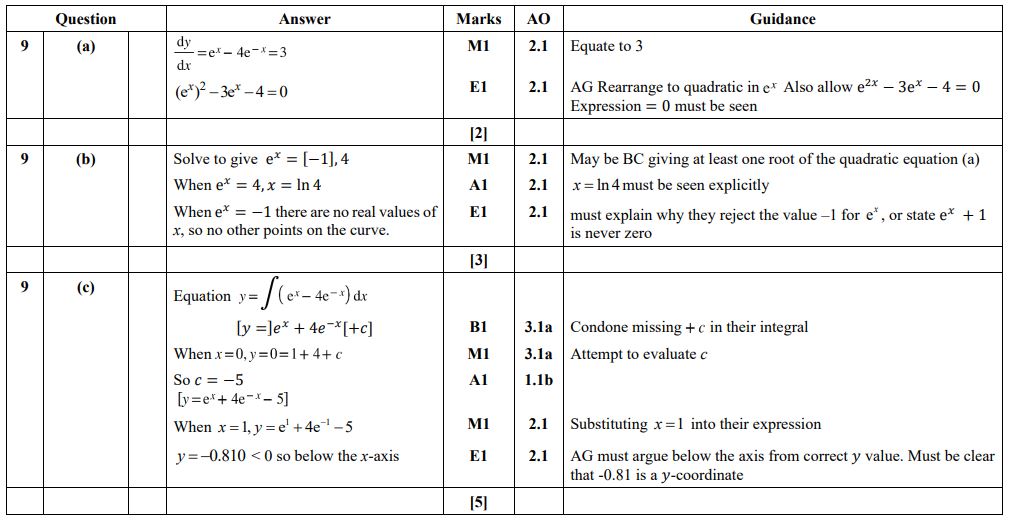
In part (a) there needs to be a clear statement that dy/dx = 3 is the starting point of the solution, and then multiplying through by e^x in order to obtain the equation in the required form.
In part (b) candidates do not only need to find the value of x where the gradient is 3, but also explicitly demonstrate that this is the only solution.
The equation of the curve needs to be found in part (c), but also a conclusion is needed that confirms that, when x = 1, the y value is negative.
To scaffold problem-solving questions
The assessment objective AO3 includes the requirement to “translate problems in mathematical and non-mathematical contexts into mathematical processes” and to “translate situations in context into mathematical models”. The “show that” is often given as a part (a), followed by the part (b) using that result as the starting point. This minimises the risk of the AO1 routine marks being inaccessible due to difficulties in the first part.
Question 5 H240/03 2023
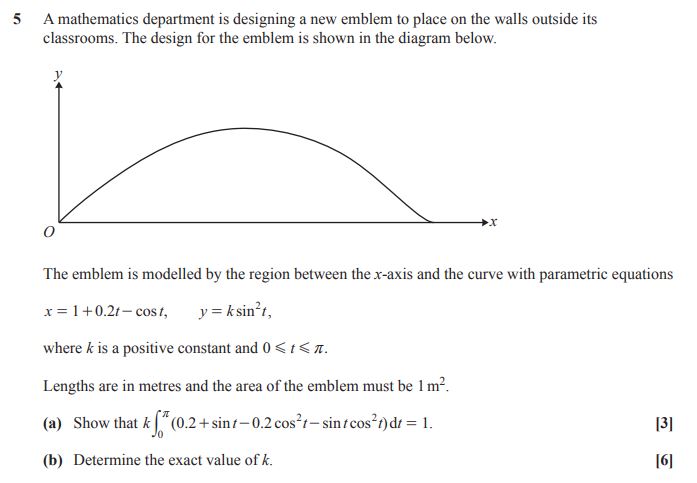
This question could have been set as a fully unstructured 9 mark question but, by splitting the question into the two parts, candidates can demonstrate their AO3 problem-solving skills in part (a) which requires them to manipulate functions defined parametrically.
Question 5(a) H240/03 2023 Mark scheme
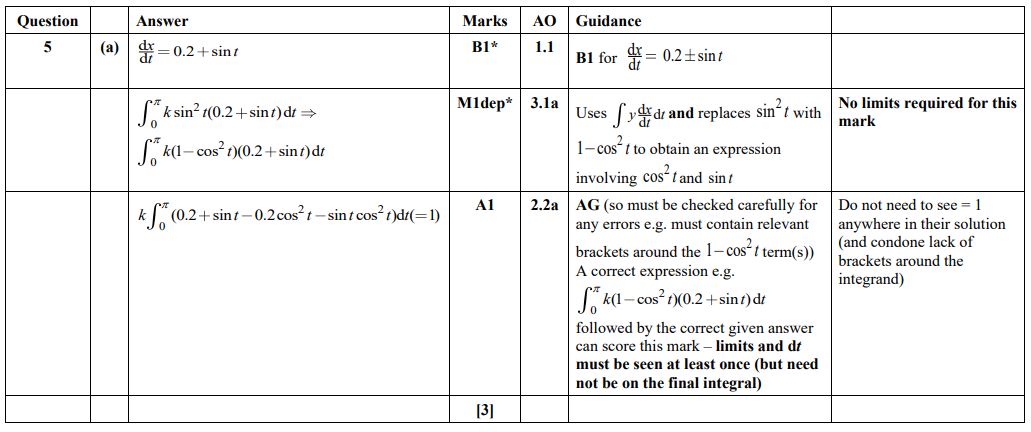
The ‘show that’ with the integration as a given answer in part (a) means that any student who faced difficulties there are not prevented from accessing the routine AO1, albeit challenging, marks in part (b).
To indicate a required answer format
There is an expectation that students should give their final answers in a simplified form. It is not unusual for questions to be set that request students to show that a given expression is the correct answer, with the requirement to ‘determine’ (Read Amy’s related blog: A deep dive into the command word ‘Determine’) the numerical values of unknowns.
Question 11 H240/01 2022
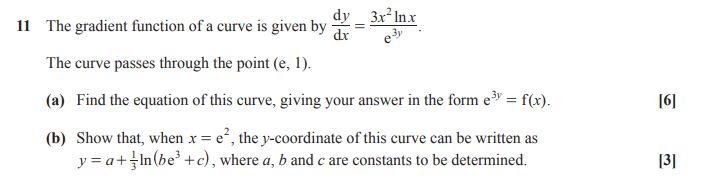
The format of the logarithmic equation required in part (b) could be simplified in a number of different ways.
Question 11(b) H240/01 2022 Mark scheme

Students will be rewarded for any correct solution, but the final A1 will only be awarded if the final answer is in the specific stated format. Not only does this help consistent marking, but students could use the given format as a hint for the direction they need to take with their solution.
Assessment hints for students
- Since the answer is given, you should state what you are calculating as well as writing down the calculation.
- Conclusions are needed to confirm how your calculations have shown that the original statement is correct.
- Only applying one step of maths in each line of the argument helps to ensure that method marks can be easily allocated and reduces the risk that multiple errors obscure any correct working.
- If you spot a sign error in your final answer then go back and correct each line of working by re-writing the incorrect lines in full, rather than crossing out individual signs.
- Even if you struggle to ‘Show that’ a statement is true, you can still use the given answer to work through the subsequent parts of the question.
Ideas for the classroom
- Initially ask the class to “find” an answer, and having had a suggested answer from one student, ask the whole class to ‘show that’ the provided answer is correct (or incorrect if appropriate).
- Use dynamic graphing to demonstrate a mathematical concept and then ask the class to generate the generalised equations required to explain the concept.
- Challenge students to show that alternate ‘simplified’ formats are equivalent in order to practice algebraic manipulation.
- Breakdown complex questions into a series of ‘Show that’ steps to scaffold the harder questions from exam papers or from the textbook.
- Remove intermediate ‘Show that’ parts to create extended response problem-solving questions.
Stay connected
Share your thoughts in the comment box below. Don’t forget to join us for our Teacher Network events.
If you have any queries, you can email us at maths@ocr.org.uk, call us on 01223 553998 or message us on X @OCR_Maths. You can also sign up to subject updates and receive information about resources and support.
If you are considering teaching any of our qualifications, use our online form to let us know, so that we can help you with more information.
About the author
Steven originally studied engineering before completing a PGCE in secondary mathematics. He has taught secondary maths in England and overseas. Steven joined OCR in 2014 and worked on the redevelopment of OCR’s FSMQ and the A Level Mathematics suite of qualifications. Steven normally drafts the weekly #OCRMathsPuzzle and then the rest of the team review, finalise and then publish each Friday. Away from the office he enjoys cooking and to travel.
Related blogs