A Level Maths: what makes a mathematical explanation?

A Level Maths: what makes a mathematical explanation? 17 December 2024

Amy Jones, Maths Subject Advisor

Amy Dai.jpg

Our A Level Maths A and B and Further Maths specifications A and B contain a list of command words along with their respective definitions. These are used throughout the question papers to help signpost students, and to provide consistent guidance for what is expected of them when answering questions. This blog looks at the use of the command word ‘Explain’ across the exam papers of both our A Level Maths suites and highlights issues to consider in teaching and when revising.

Ordinary English meaning

The specifications only define ‘Explain’ as having its ordinary English meaning, but what does that mean in terms of a maths question? The dictionary suggests that ‘Explain’ means to:

Make a situation clear by revealing relevant facts.
Make an idea clear by describing it in more detail.
Give a reason to justify a result.
Interpret a result in the context of the original problem.

Explain is often used as an initial, or final part of a question and is generally only worth 1 or 2 marks. Examiners note that these parts of questions are frequently left blank, with candidates focused on the calculations rather than writing sentences. Across the paper, or even the whole assessment, these individual marks can add up – showcasing why it is important for candidates to attempt these question parts.

When marking candidate responses, examiners will not be looking for an essay, usually bullet points will be sufficient. There is also a risk that an extended response might contain contradictions, so a concise approach is recommended. Remember that this is a maths exam so the response should include calculations, equations or sketched graphs if relevant.

Pure Maths

‘Explain’ is often used in pure maths questions, usually those without a context, to assess students’ understanding of the fundamental principles behind a concept. It is important to ensure responses do not involve any contradictions and are specific to the set question.

Image of question 10(a) of H240/01 from 2023. A sketch of the function defined in the question is given. The sketch shows a discontinuous function with a positive root near x = 0.3.

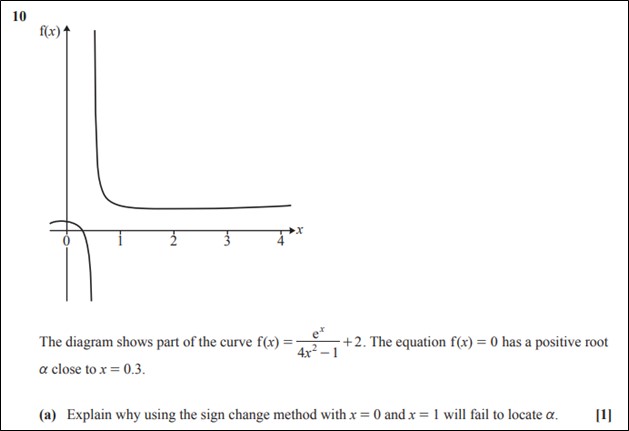
Q10(a) H240/01 2023

There are a number of reasons why a sign change method might fail to locate a root, so the response needs to relate to the given function. It was expected that students would mention that the values for f(0) and f(1) do not show a change in sign.

Image of the mark scheme for question 10(a) of H240/01 from 2023. The mark scheme details guidance around when to award the B1 mark.

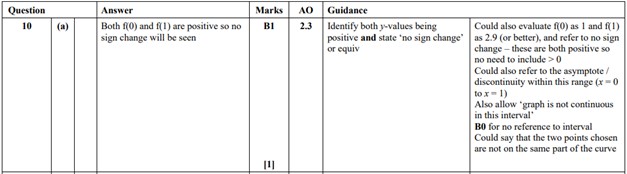
Mark scheme Q10(a) H240/01 2023

Simply stating that the curve is discontinuous would not be sufficient. In order to gain credit the response would need to emphasise that the curve is discontinuous between x = 0 and x = 1 therefore both f(0) and f(1) would be positive.

Image of question 12(a) of H640/02 from 2023. Three different equations are given along with their domains.

Q12(a) H640/02 2023

Students are asked to demonstrate their depth of understanding of functions by giving a reason to justify the stated result in the question.

Image of the mark scheme for question 12(a) of H640/02 from 2023. Guidance is given for when to award the B1 mark, including an explicit example of when not to award the mark.

Mark scheme Q12(a) H640/02 2023

Notice that any response that includes anything along the lines of ‘it is a one-to-many function’ will not gain credit, as this would contradict the question. Giving numerical examples, perhaps within a mapping diagram, would be helpful in supporting any valid response.

Pure content may also contain an assessment in mathematical modelling of a ‘real-life’ application of maths. ‘Explain’ is often used to evaluate when a proposed model is either valid or invalid.

Image of question 15 of H630/02 from 2023. The question includes five sub-parts. The whole question is based around a context of a family planning a holiday.

Q15 H630/02 2023

In part (d), the question is looking for a reason, in context, for why the model would be invalid when t is large.

Image of the mark scheme for question 15(d) of H630/02 from 2023. There is guidance about what is required in the candidate response to be awarded B1.

Mark scheme Q15(d) H630/02 2023

Comments related to factors outside of the model in the question (geo-political, pandemic etc) would not gain credit. The response must relate to the question, in this case to the exchange rate values obtained when larger values of t are considered. It is good practice to actually state some calculated values to demonstrate the limitations.

Statistics

It is important that explanations relate to the statistical evaluation being undertaken in the context of the question and not simply generic textbook definitions.

Image of question 10 of H230/02 from 2023 showing questions related to a histogram. The histogram is included in the question.

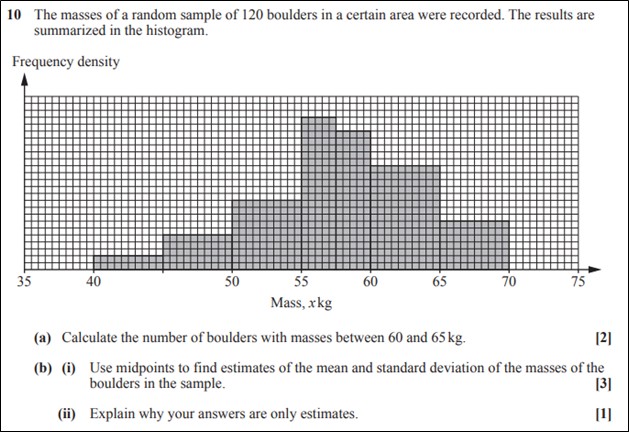
Q10 (b)(ii) H230/01 2023

This question is probing students’ understanding of the limitations of graphical representations of data.

Image of mark scheme for question 10(b)(ii) of H230/02 from 2023. It gives guidance for what is required for the B1 mark to be awarded.

Mark scheme Q10 (b)(ii) H230/01 2023

“Candidates should be reminded that Explain questions require an explanation that is specific to the question being asked (often, in context). The request is for candidates to demonstrate their understanding in the context of the question, not to state a fact.”

Examiners’ report. H230/01, 2023

As exemplified in the comment above, it is important that the reason given is not just true but is relevant to the specific question asked. The midpoints are used on the assumption that the data within each group is uniformly distributed, but the calculation from the histogram is only an estimate because we don’t know how the data within each bar is actually distributed.

Mechanics

As with statistics, it is important that explanations relate to the specific aspect of the mathematical model referred to in the question, and not just a fact that is true about the model.

Image of question 4 of H640/01 from 2023 showing questions related to a uniform lamina. The question includes a diagram of a ruler along with the force affecting it.

Q4 H640/01 2023

Part (a) involved a moments about P calculation, 0.02g × 15 = F × 4, so part (b) is looking for students to make clear that without F there is nothing opposing the 0.02g × 15 moment acting clockwise about P. Precise language is needed; the response ‘fall down’ could mean falling vertically which would not be correct.

Image of mark scheme for question 4(b) of H640/01 from 2023. Additional guidance is provided to detail what is required for a response to be given a B1 mark.

Mark scheme Q4b H640/01 2023

Ideas for the classroom

Go beyond the “Explain” questions asked in exam questions to consider other limitations of the mathematical model used in that context.
Discuss how those limitations could be addressed in practice, and the implications of those proposals (cost, mathematical complexity etc).
When discussing an exam question as a class (either as a starter, model answer or plenary), at the end ask the students how they would add an “Explain” question on at the end. Then you can discuss what an appropriate response would be for the different “Explain” questions that have been suggested.

Stay connected

Share your thoughts in the comments below. Don’t forget to join us for our Teacher Network events. If you have any questions, you can email us at maths@ocr.org.uk, call us on 01223 553998 or message us on X @OCR_Maths. You can also sign up for monthly email updates to receive information about resources and support.

If you are considering teaching any of our qualifications, use our online form to let us know, so that we can help you with more information.

About the author

Amy (previously Amy Dai) joined OCR in 2023 after teaching for five years in both state and independent schools. She provides support across all the OCR Maths qualifications, but with a focus on GCSE, A Level Maths and Further Maths. She graduated from the University of York with a degree in Mathematics and Economics before gaining a PGCE in Secondary Mathematics and an MA in Education.

Main navigation