A Level Mathematics specification B (MEI) – what's in it for you?
28 August 2023
Steven Walker, Maths Subject Advisor
This blog has been updated with new links to Teach Cambridge, our new secure resource platform.
We offer two versions of both our A Level Maths qualifications, one designed entirely by OCR and the other developed in partnership with respected curriculum body Mathematics in Education and Industry (MEI).
- Spec A (H230, H235, H240 and H245) is produced by OCR independently
- Spec B (H630, H635, H640 and H645) is produced in partnership with MEI.
No two students are identical and having two specifications allows us to produce qualifications that offer choice to centres in order to deliver the course that suits the particular needs of their students. While much of the content is similar across the two specifications, there are differences in the structure, emphasis, and approaches to assessment.
Both suites are administered by OCR and any queries about the exams should be directed to us. Amy, Ruth, Neil, Caroline and myself are always happy to help. Email any questions to maths@ocr.org.uk. We may not know every answer, but we should know who does.
Partnerships and collaborations
OCR has a long tradition of working with subject bodies and individual experts to develop either qualification specifications and/or support resources. A Level Mathematics and Further Mathematics are two such subjects where OCR offers a ‘traditional’ specification A and also a second specification B developed in collaboration with a leading curriculum support organisation.
What is MEI’s role in spec B?
MEI is a long-established, independent curriculum development body. As part of their advocacy role they were involved in the original stakeholder discussions on the reform of A Level Maths and Further Maths. Throughout the development process they have continuously consulted with teachers and representatives from Higher Education to build on their popular legacy MEI A Level Mathematics suite.
In addition to the support and professional development provided through OCR you will also be able to access support from MEI through the MEI Staffroom.
For specific curriculum queries, email Keith Proffitt, who is responsible for supporting teachers of OCR B (MEI) AS and A Levels with professional development, resources, and advice.
What are the common features of spec A and spec B?
Both specifications are set out to highlight clear progression from AS to A Level and from Maths to Further Maths.
Both use the same set of examination command words. This means a large proportion of questions from one spec could be used to create topic tests for students studying the other spec (see ExamBuilder).
Both suites use separate question papers and printed answer booklets so that candidates can see each full question and their answers to ensure any question scaffolding is not lost through page turning.
There are no multiple choice questions in the assessment of either of these suites. Candidates will be rewarded for their attempts rather than simply penalised for errors.
Both Further Maths specifications allow candidates to sit additional optional components for a broader curriculum. Grading will automatically identify the best grading combination.
Both Maths qualifications include the formulae sheet at the start of each question paper. The Further Maths qualifications do have a separate formulae booklet that incorporates all the formulae (Maths and Further Maths). This means that candidates only studying Maths are not swamped by additional material that is not needed. It is very rare that a question on the Maths paper could be answered more quickly using a technique only covered in the Further Maths course, so not providing the additional formulae also removes the temptation, often attempted badly, to adapt inappropriate advanced techniques.
Exam papers and resources for both specifications are available to all teachers signed up to Teach Cambridge.
We run a full programme of professional development for each specification, but our teacher networks bring together teachers from both specifications for more general discussions on maths themes.
The unique approach in Maths B (MEI) – H640
Pure and applied
The first thing that can be seen on H640/01 and H640/02 is that pure and applied questions are mixed throughout the papers. Candidates start these papers with a collection of routine, short answer questions in section A. These provide a gentle introduction to the exam session, and give candidates the opportunity to demonstrate skills in both the pure and the applied content (H640/01 Pure and Mechanics, H640/02 Pure and Statistics), before moving on to more in-depth questions that may involve problem-solving in section B. This design allows a gradient of demand from start to finish rather than increasing to a peak and then dropping back down half way through the paper.
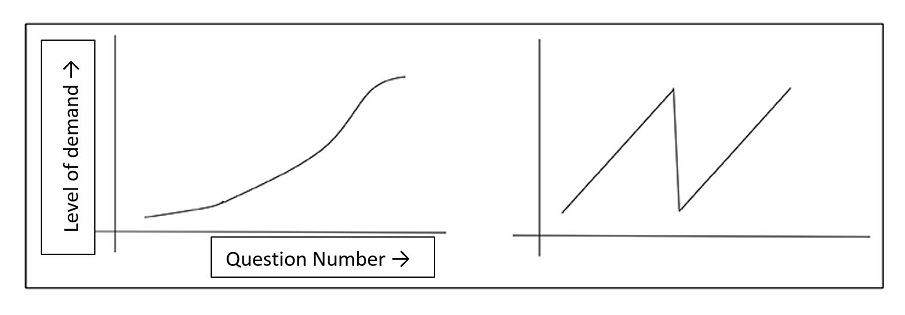
Mixing the pure and applied questions also blurs the artificial demarcation between the strands, encouraging a more synoptic approach to the teaching and learning of mathematics.
Large data set
One of the requirements of the DfE A Level Maths content criteria was that students must become familiar with one or more specific large data sets (LDS) in advance of the final assessment so that they gain experience of using technology to investigate and interpret real data.
Providing multiple data sets ensures that students recognise that the learned techniques are applicable across the range of contexts, and regularly updating the LDS ensures students can refer their calculations to current events.
See Keith’s blog about three large data sets for more information on the MEI approach to the LDS.
The comprehension section
The purpose of A Level Mathematics is defined in the content criteria as supporting students’ mathematical needs across a broad range of subjects, emphasising how mathematical ideas are interconnected, how maths can be used to model situations to understand data and the physical world, and how it can used to solve problems in a variety of contexts.
All accredited A Level Maths qualifications must set some questions that assess these skills. H640/03 has a clearly defined Section B ‘comprehension’ article, with factored in ‘reading time’ for this aspect of the qualification.
See my Preparing for the comprehension section blog for some teaching and learning ideas for supporting students with this requirement.
Incorporating technology and real life contexts
A slightly more subtle difference between the assessment of the MEI specification compared to more traditional approaches is the use of screen shots from software applications, rather than using tables and graphs.
Question 6 Sample Assessment Material H640/01
Fig. 6 shows a partially completed spreadsheet which uses the trapezium rule with four strips to estimate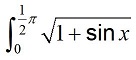 
|
A
|
B
|
C
|
D |
E |
| 1 |
|
x
|
sin x
|
y
|
|
2
|
0
|
0.0000
|
0.0000
|
1.0000
|
0.5000
|
3
|
0.125
|
0.3927 |
0.3827 |
1.1759 |
0.1759 |
4
|
0.25
|
0.7854 |
0.7071 |
1.3066 |
0.3066 |
5
|
0.375
|
1.1781 |
0.9239 |
1.3870 |
1.3870 |
| 6 |
0.5
|
1.5708 |
1.0000 |
1.4142 |
0.7071 |
| 7 |
|
|
|
|
5.0766 |
| 8 |
|
|
|
|
|
Fig. 6
- Show how the value in cell B3 is calculated. [1]
- Show how the value in cell E7 is calculated from the values in cells D2 to D6 [1]
- Complete the calculation to estimate 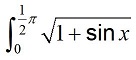, giving the answer to 3 significant figures. [2]
The unique approach in Further Maths B (MEI) – H645
The DfE A Level Further Maths content criteria fixed 50% of the content as mandatory pure content, leaving the specification designers to construct optional routes for the other 50%. A Level Further Maths B(MEI) has more than just the standard Further Statistics, Further Mechanics and Discrete options. There are three routes through the MEI specification. Routes A and B include a major component of either mechanics or statistics with a choice of minor components. Route C allows students to study three different minor components for greater breadth of study.
Major or minor options
The most popular components of Mechanics and Statistics can be studied as either major or minor options (where the content of the major is of the size comparable to two minors). The major options allow students to develop a depth of study.
Mechanics minor introduces the concepts of dimensional analysis, forces in equilibrium on particles and rigid bodies, work, energy and power, momentum and impulse involving direct collisions, and centre of mass of systems of particles and some given shapes to solve problems involving equilibrium of rigid bodies. This content is expanded in the major component with oblique impact collisions, circular motion, Hooke’s Law, using volume of rotation calculus in centre of mass problems and calculus in kinematics problems in more than one dimension or with variable forces.
Statistics minor investigates discrete random variables, bivariate data and Chi-squared tests. The major component expands the work of this and the Maths A level to cover continuous random variables, inference and simulations.
Broader range of options
Mechanics and Statistics are two of the six available options in Further Maths B(MEI) – H645.
Modelling with Algorithms differs from Decision or Discrete Maths options in that it is more focused on the application of techniques to solve real world problems than just looking at the theory of graphs and networks.
Numerical Methods looks beyond the traditional search for exact solutions, reflecting the fact that there may not be a nice neat analytical solution to real life problems. In this option students apply numerical approaches to four topics from mathematics: solution of equations, differentiation, integration, and approximating functions. The course encourages the use of spreadsheets and also to analyse the associated errors of these approximations.
Extra Pure introduces concepts which are foundational in undergraduate mathematics: revealing unexpected connections between different parts of mathematics, investigates underlying structure and provides a suitable end point for some topics introduced within the mandatory component.
Further Pure with Technology takes students into 21st century mathematics, using a computer algebra system, a spreadsheet, a graph plotter and a programming language to investigate curves, explore topics in number theory and explore the solutions to families of differential equations analytically and numerically.
Stay connected
If you have any queries you can email us at maths@ocr.org.uk, call us on 01223 553998 or tweet us @OCR_Maths. You can also sign up for monthly email updates to receive information about resources and support.
About the author
Steven joined OCR in 2014 during the major qualification reform period and now primarily focus on supporting the Level 3 maths qualifications. He originally studied engineering and then took an extended period to work and travel around the world before completing a PGCE in secondary mathematics. Steven began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas. He taught the legacy MEI Mathematics units Core 1, Core 2, Core 3, Core 4, Mechanics 1, Mechanics 2, Statistics 1, Discrete 1 and Further Pure 1 and regularly attends the MEI annual conferences.
By the same author